<0x09> 挖地雷
题目描述
在一个地图上有 $N\ (N \le 20)$ 个地窖,每个地窖中埋有一定数量的地雷
同时,给出地窖之间的连接路径
当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后可以沿着指出的连接往下挖(仅能选择一条路径)
当无连接时挖地雷工作结束
设计一个挖地雷的方案,使某人能挖到最多的地雷
输入格式
有若干行。
第 $1$ 行只有一个数字,表示地窖的个数 $N$
第 $2$ 行有 $N$ 个数,分别表示每个地窖中的地雷个数
第 $3$ 行至第 $N+1$ 行表示地窖之间的连接情况:
第 $3$ 行有 $n-1$ 个数($0$ 或 $1$),表示第一个地窖至第 $2$ 个、第 $3$ 个 $\dots$ 第 $n$ 个地窖有否路径连接
如第 $3$ 行为 $11000\cdots 0$,则表示第 $1$ 个地窖至第 $2$ 个地窖有路径,至第 $3$ 个地窖有路径,至第 $4$ 个地窖、第 $5$ 个 $\dots$ 第 $n$ 个地窖没有路径
第 $4$ 行有 $n-2$ 个数,表示第二个地窖至第 $3$ 个、第 $4$ 个 $\dots$ 第 $n$ 个地窖有否路径连接
……
第 $n+1$ 行有 $1$ 个数,表示第 $n-1$ 个地窖至第 $n$ 个地窖有否路径连接
(为 $0$ 表示没有路径,为 $1$ 表示有路径)
输出格式
第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个空格分隔,不得有多余的空格
第二行只有一个数,表示能挖到的最多地雷数
样例
样例输入
5
10 8 4 7 6
1 1 1 0
0 0 0
1 1
1
样例输出
1 3 4 5
27
分析
貌似可以用DFS过(题解也有人说能),但为了练动态规划就没去用
怎么动态规划呢,关键还是状态转移方程
令状态转移方程为$f(i)$,$i$表示到下标为$i$的地窖停止
令下标为$i$的地窖有地雷$a_i$个
所以状态转移方程为$f(i)=a_i+max(a_1,…,a_{i-1})$
代码
#include <iostream>
#include <vector>
int n;
std::vector<int> nums;
// 定义搜索信息类
class SearchInfo
{
std::vector<int> searchList;
int count = 0;
public:
SearchInfo()
{
searchList.clear();
}
SearchInfo(int index)
{
searchList.push_back(index);
count += nums[index];
}
SearchInfo(const SearchInfo &c)
{
searchList.assign(c.searchList.begin(), c.searchList.end());
count = c.count;
}
void Println()
{
for (auto &i : searchList)
{
std::cout << i + 1 << " ";
}
std::cout << "\n";
std::cout << count << "\n";
}
bool operator>(const SearchInfo &r) const
{
return count > r.count;
}
bool operator<(const SearchInfo &r) const
{
return count < r.count;
}
SearchInfo Append(int index)
{
SearchInfo ans(*this);
ans.searchList.push_back(index);
ans.count += nums[index];
return ans;
}
static SearchInfo Max(SearchInfo a, SearchInfo b)
{
return a > b ? a : b;
}
};
std::vector<std::vector<bool>> map;
std::vector<SearchInfo> dp;
int main()
{
std::cin >> n;
nums.resize(n);
map.resize(n);
dp.resize(n);
for (int i = 0; i < n; i++)
{
std::cin >> nums[i];
map[i].resize(n, false);
}
for (int i = 0; i < n - 1; i++)
{
for (int j = i + 1; j < n; j++)
{
int temp;
std::cin >> temp;
map[i][j] = temp == 0 ? false : true;
map[j][i] = temp == 0 ? false : true;
}
}
dp[0] = SearchInfo(0);
// 关键DP方程
for (int i = 1; i < n; i++)
{
for (int j = 0; j < i; j++)
{
// 有路的时候
if (map[i][j])
{
dp[i] = SearchInfo::Max(dp[i], dp[j]);
}
}
// 附加上
dp[i] = dp[i].Append(i);
}
SearchInfo max;
for (int i = 0; i < n; i++)
{
if (dp[i] > max)
{
max = dp[i];
}
}
max.Println();
return 0;
}
遇到的坑
经验不足,想状态转移方程方向出了点问题
我原本是认为是定义$f(i,j)$其中$i$表示扫了几个房间的雷,$j$表示从哪个房间开始
没想出来。所以稍微看了眼题解的状态转移方程,恍然大悟
这个也没啥办法,动态规划只是一种思想,要熟练得多练
还有,这题貌似是单向的搜索,因为按照代码的思路,是得不出1 3 2 5 4这样的路径的
这里给出测试样例
5
1 2 3 4 5
0 1 0 0
1 0 1
0 0
1
按道理挖雷最大化路径就是1 3 2 5 4,但代码会给出4 5
考虑到洛谷那边确实是过了,那应该是我之前的理解也有问题
我默认当成是一笔画问题去考虑,想状态方程也是重点往这方面想,一直也想不出来
估计做这题还是记忆化搜索保险,要真是一笔画思路的话这样写就过不了了
<0x0A> 今日题目:过河卒
不知不觉写了10天了,目前只能说C++没之前这么手生了
算法的话也算稍微接触了下动态规划,学到了很多
洛谷的P1002
题目描述
棋盘上 $A$ 点有一个过河卒,需要走到目标 $B$ 点
卒行走的规则:可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点
因此称之为“马拦过河卒”。
棋盘用坐标表示,$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$,同样马的位置坐标是需要给出的
达 $B$ 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步
输入格式
一行四个正整数,分别表示 $B$ 点坐标和马的坐标。
输出格式
一个整数,表示所有的路径条数。
样例
样例输入
6 6 3 3
样例输出
6
数据规模与约定
对于 $100 %$ 的数据,$1 \le n, m \le 20$,$0 \le$ 马的坐标 $\le 20$。
分析
可以当成动态规划题目来看
因为只能往下/往右走,不存在回头的可能
所以可以将问题分解成到上一格怎么走,上上格怎么走
比方说(0,0)→(3,2)就可以分解成(0,0)→(2,2)+(3,1)→(3,2),以此类推
这样就很像之前写的数楼梯的题了
记(0,0)→(0,0)的路径数为1
那么可以写出状态转移方程$f(x,y)=f(x-1,y)+f(x,y-1),f(0,0)=1$
这样的话遍历一遍整个地图就可以了
代码
#include <iostream>
#include <vector>
// 我习惯封装一个地图
class Map
{
std::vector<std::vector<int>> mat;
public:
Map(int n)
{
mat.resize(n);
for (int i = 0; i < n; i++)
{
mat[i].resize(n, 0);
}
}
int &At(int x, int y)
{
return mat[y][x];
}
void Set(int x, int y, int num)
{
if (x < 0 || y < 0)
{
return;
}
if (x >= mat.size() || y >= mat.size())
{
return;
}
mat[y][x] = num;
}
int Length()
{
return mat.size();
}
};
Map map(22);
int ex, ey;
size_t dp[22][22];
int main()
{
int hx, hy;
std::cin >> ex >> ey >> hx >> hy;
// 这样方便算递推
dp[1][1] = 1;
ex++;
ey++;
hx++;
hy++;
map.At(hx, hy) = 1;
// 设置马的8个方向
map.Set(hx - 1, hy - 2, 1);
map.Set(hx + 1, hy - 2, 1);
map.Set(hx + 2, hy - 1, 1);
map.Set(hx + 2, hy + 1, 1);
map.Set(hx - 1, hy + 2, 1);
map.Set(hx + 1, hy + 2, 1);
map.Set(hx - 2, hy - 1, 1);
map.Set(hx - 2, hy + 1, 1);
// 开始递推
for (int i = 1; i <= ex; i++)
{
for (int j = 1; j <= ey; j++)
{
// 跳过第一个点
if (i == 1 && j == 1)
{
continue;
}
if (map.At(i, j) != 1)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
std::cout << dp[ex][ey] << "\n";
return 0;
}
遇到的坑
我最开始看到这道题我以为问题不大
所以就直接拿出DFS了,DFS也算递归嘛
然后就有两个数据点没过
后来一想就发现问题了,既然不要求路径,那也没必要用DFS,直接递推就可以了
<0x0B> 最大食物链计数
这几天有别的事情忙,所以算法练习就搁置了几天
洛谷的P4017
题目背景
你知道食物链吗?Delia 生物考试的时候,数食物链条数的题目全都错了
因为她总是重复数了几条或漏掉了几条 于是她来就来求助你,然而你也不会啊!写一个程序来帮帮她吧。
题目描述
给你一个食物网,你要求出这个食物网中最大食物链的数量。
(这里的“最大食物链”,指的是生物学意义上的食物链,即最左端是不会捕食其他生物的生产者,最右端是不会被其他生物捕食的消费者。)
Delia 非常急,所以你只有 $1$ 秒的时间。
由于这个结果可能过大,你只需要输出总数模上 $80112002$ 的结果。
输入格式
第一行,两个正整数 $n、m$,表示生物种类 $n$ 和吃与被吃的关系数 $m$。
接下来 $m$ 行,每行两个正整数,表示被吃的生物A和吃A的生物B。
输出格式
一行一个整数,为最大食物链数量模上 $80112002$ 的结果。
样例
样例输入
5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4
样例输出
5
数据规模与约定
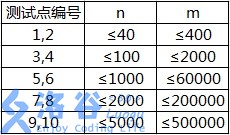
数据中不会出现环,满足生物学的要求。
分析
这道题的关键在于拓扑排序
拓扑排序的概念可以看OI Wiki的介绍
为什么要拓扑排序呢,因为对于这种很像之前写的过河卒的题目
递推公式可以是这样$f(v)=\sum_{i是可以到达v的顶点}(f(i))$
拓扑排序可以获得这样的顺序,保证我们在计算某节点时,需要的数据都已经计算过
得到顺序之后还需要获得原图的逆转图
因为我们需要可以到达某顶点的信息,如果遍历全图去找的化开销太大
还不如直接从逆转图中获取
最后根据递推公式计算出到达终点的路径总数
因为题目没说只有一个终点,所以还需要把所有终点的值加起来
记得按要求取模,答案也就出来了
代码
// 因为带各种封装,所以代码就有点长
#include <iostream>
#include <stack>
#include <vector>
// 表示图的类
class Graph
{
// 存储图的数据,采用邻接表数组表示
std::vector<std::vector<int>> _list;
// 记录每个顶点的出度
std::vector<int> _out;
// 顶点总数
int _vertexCount;
public:
Graph(int num)
{
_vertexCount = num;
_list.resize(num);
_in.resize(num, 0);
_out.resize(num, 0);
}
int VertexCount() const
{
return _vertexCount;
}
// 添加边
void AddEdge(int v, int w)
{
for (auto i : _list[v])
{
if (i == w)
{
return;
}
}
_list[v].push_back(w);
_out[v]++;
}
// 获取出度为0的顶点
std::vector<int> GetEnd()
{
std::vector<int> ans;
for (int i = 0; i < _out.size(); i++)
{
if (_out[i] == 0)
{
ans.push_back(i);
}
}
return ans;
}
// 获取从该顶点的可到达的下一个顶点
std::vector<int> AdjoinVertex(int v) const
{
return std::vector<int>(_list[v]);
}
// 获取反向的图
Graph InverseGraph(const Graph &G)
{
int length = G._vertexCount;
Graph ans(length);
for (int v = 0; v < length; v++)
{
for (auto w : _list[v])
{
ans.AddEdge(w, v);
}
}
return ans;
}
};
// 拓扑排序的类
class Topological
{
// 记录逆后续
std::stack<int> _reversePost;
// 记录答案
std::vector<int> _list;
// 标记是否走过
std::vector<bool> _marked;
// 通过DFS法获得拓扑排序
void DFS(const Graph &G, int v)
{
_marked[v] = true;
std::vector<int> temp = G.AdjoinVertex(v);
for (auto w : temp)
{
if (!_marked[w])
{
DFS(G, w);
}
}
_reversePost.push(v);
}
public:
// 构造函数中就完成拓扑排序
Topological(const Graph &G)
{
int length = G.VertexCount();
_marked.resize(length, false);
for (int i = 0; i < length; i++)
{
if (!_marked[i])
{
DFS(G, i);
}
}
// DFS结束后保存结果
while (!_reversePost.empty())
{
_list.push_back(_reversePost.top());
_reversePost.pop();
}
}
std::vector<int> GetAns()
{
return _list;
}
};
int main()
{
// 读入
int n, m;
std::cin >> n >> m;
Graph g(n);
int v, w;
for (int i = 0; i < m; i++)
{
std::cin >> v >> w;
// 记得减一
g.AddEdge(v - 1, w - 1);
}
// 求出拓扑排序
Topological topo(g);
auto order = topo.GetAns();
Graph ig = g.InverseGraph(g);
// 初始化递推
std::vector<size_t> ans;
ans.resize(n, 0);
for (auto i : order)
{
std::vector<int> temp = ig.AdjoinVertex(i);
if (temp.size() == 0)
{
ans[i] = 1;
continue;
}
for (auto j : temp)
{
ans[i] += ans[j];
}
ans[i] %= 80112002;
}
size_t o = 0;
// 因为题目没说只有一个终点,所以还要这样遍历一下
for (auto i : g.GetEnd())
{
o += ans[i];
o %= 80112002;
}
std::cout << o << "\n";
return 0;
}
<0x0C> 摆花
题目描述
小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 $m$ 盆
通过调查顾客的喜好,小明列出了顾客最喜欢的 $n$ 种花,从 $1$ 到 $n$ 标号
为了在门口展出更多种花,规定第 $i$ 种花不能超过 $a_i$ 盆
摆花时同一种花放在一起,且不同种类的花需按标号的从小到大的顺序依次摆列。
试编程计算,一共有多少种不同的摆花方案。
输入格式
第一行包含两个正整数 $n$ 和 $m$,中间用一个空格隔开。
第二行有 $n$ 个整数,每两个整数之间用一个空格隔开,依次表示 $a_1,a_2, \cdots ,a_n$。
输出格式
一个整数,表示有多少种方案。注意:因为方案数可能很多,请输出方案数对 $10^6+7$ 取模的结果。
样例
样例输入
2 4
3 2
样例输出
2
数据规模与约定
对于 $20%$ 数据,有 $0<n \le 8,0<m \le 8,0 \le a_i \le 8$。
对于 $50%$ 数据,有 $0<n \le 20,0<m \le 20,0 \le a_i \le 20$。
对于 $100%$ 数据,有 $0<n \le 100,0<m \le 100,0 \le a_i \le 100$。
分析
(也可以用记忆化搜索,不过考虑到练dp这里就不使用)
这是一道动态规划题
虽然看着不像是动态规划,倒是挺像递推的题
属于是计数dp的类型,思路上确实接近递推
定义状态转移方程$f(i,j)=\sum_{t=0}^{a_i}f(i-1,j-t)$
其中$i$表示前$i$种花,$j$表示已经放了$j$盆花
怎么理解这个状态转移方程呢
因为题目的限制,我们只需要考虑每种花要摆几盆即可
对于每次递推,我们可以想象成给一串珠子再串一个珠子的过程
假设前面已有的接法有$x$种,要到目标盆数$y$,则还需要$y-x$盆这个数是固定的
也就是前面有$x$种可能,后面只有1种可能,那么直接加$x$即可
代码
#include <iostream>
#include <vector>
int main()
{
// 读入
int n, m;
std::cin >> n >> m;
std::vector<int> list(n);
for (int i = 0; i < n; i++)
{
std::cin >> list[i];
}
// 初始化,注意map的第二维需要多一个空间
std::vector<std::vector<size_t>> map;
map.resize(n, std::vector<size_t>(m + 1));
// 初始化第一种花的情况
for (int i = 0; i <= list[0]; i++)
{
map[0][i] = 1;
}
// 开始dp
for (int i = 1; i < n; i++)
{
for (int j = 0; j <= m; j++)
{
map[i][j] = 0;
for (int t = 0; j - t >= 0 && t <= list[i]; t++)
{
map[i][j] += map[i - 1][j - t];
map[i][j] %= 1000007;
}
}
}
// 输出最后的结果
std::cout << map[n - 1][m] << "\n";
return 0;
}